
"All models are wrong, but some are useful."- George E.P. Box
LAYER POTENTIAL METHODS FOR HARMONIC FUNCTIONS ON FINITELY CONNECTED TORI

Collaborating with Dr. Braxton Osting (University of Utah, Math)
Kim, B., Osting, B. (2024, preprint). Integral Equation Methods for Harmonic Functions on Finitely-Connected Tori. [Code] [Poster]
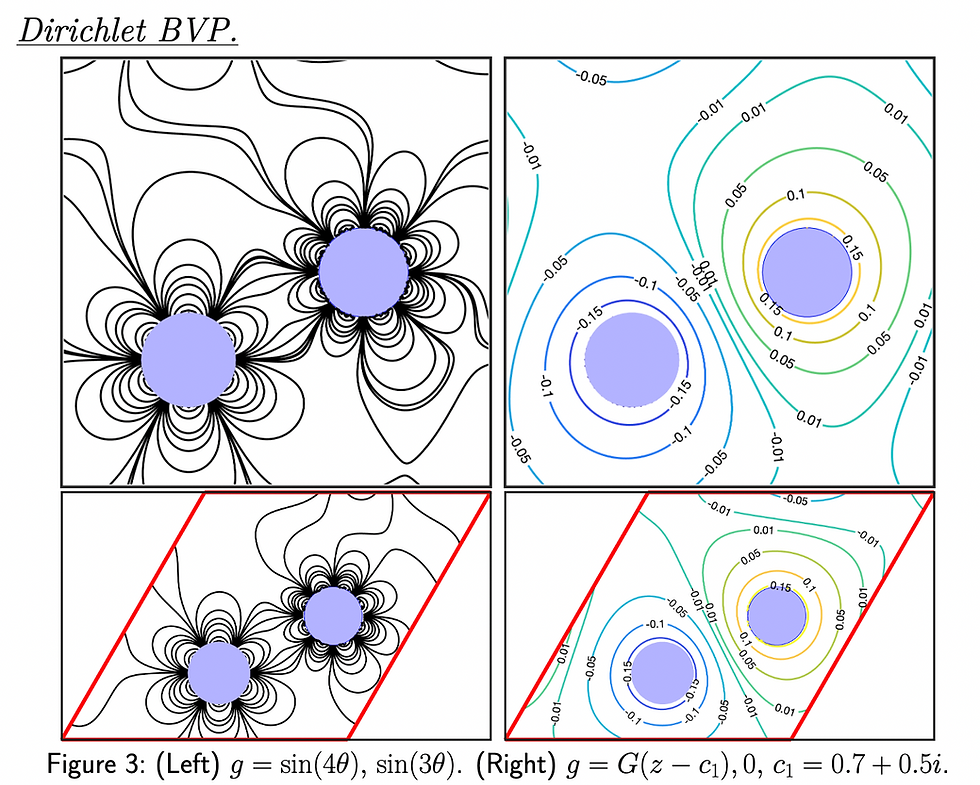
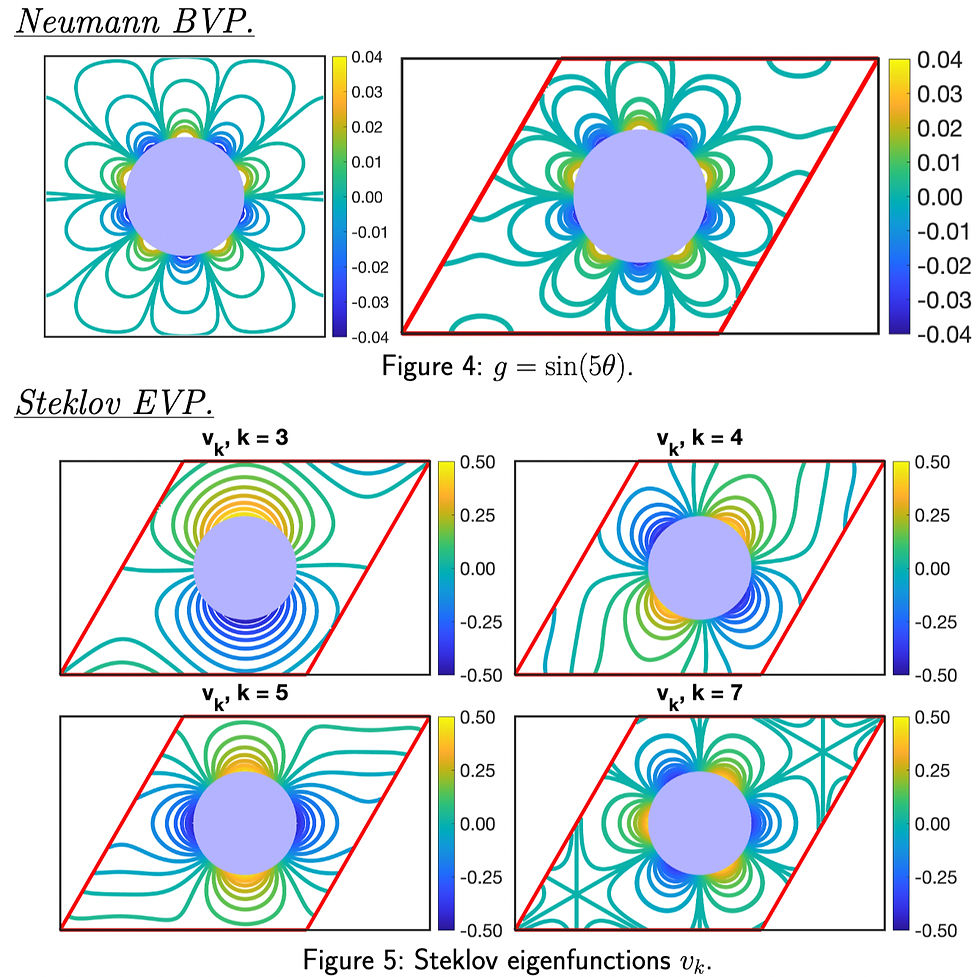
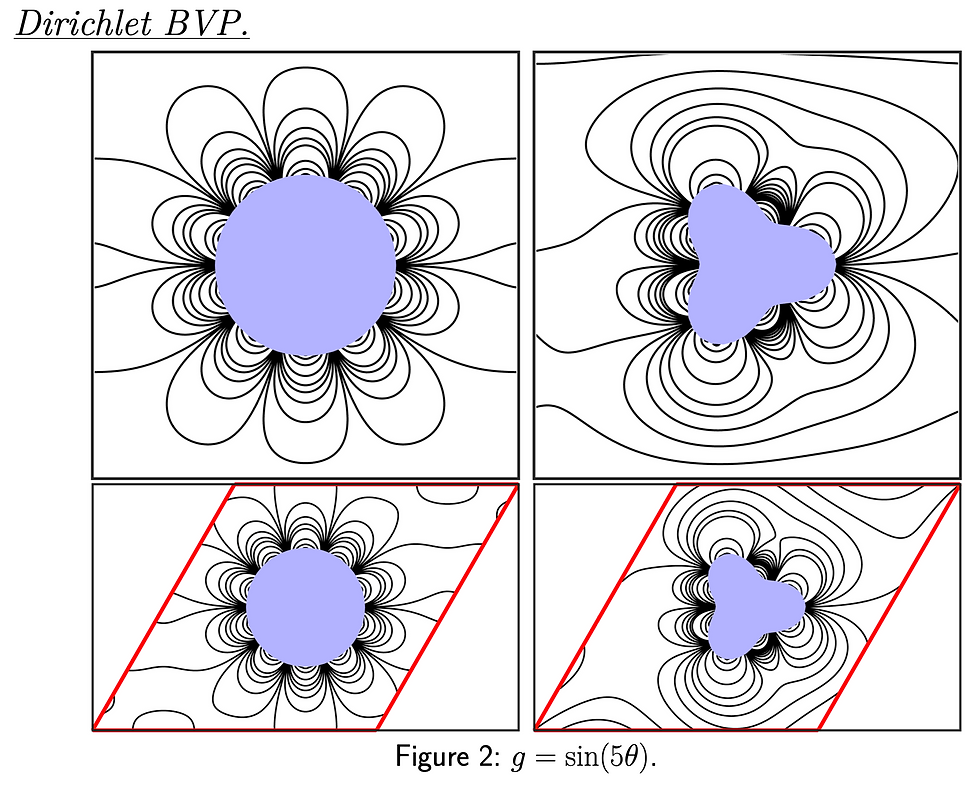
We develop layer potential methods to represent harmonic functions on finitely-connected tori. Extending the results for Euclidean domains, we represent the doubly-periodic Green's function using the Jacobi theta function and analyze the resulting single- and double-layer potentials. The cases where the boundary has one connected component and multiple connected components are handled separately. We apply our developed theory to approximate solutions of the Dirichlet and Neumann boundary value problems, as well as the Steklov eigenvalue problem. We implement the developed methods and demonstrate the theory with several numerical examples.
Numerical Methods for Partial Differential Equations (PDE) arising in fiber coating (Ph D. Thesis)
Collaborating with
Dr. Hangjie Ji (NC States, Math)
Dr. Andrea L. Bertozzi (UCLA, Math)
Dr. Abolfazel Sadeghpour (UCLA, Mechanical Engineering)
Dr. Y. Sungtaek Ju (UCLA, Mechanical Engineering)
Kim, B., Ji, H., Bertozzi., A., Sadeghpour A., Ju, S. “A positivity-preserving numerical method for a thin liquid film on a vertical cylindrical fiber (2023).” In Journal of Computational Physics. [Paper] [Software][Poster]
Kim, B. “Theory of Positivity-Preserving Numerical Methods for Thin Viscous
Liquids Flowing Down Vertical Fibers” PhD thesis, University of California, Los
Angeles, 2023. [Link]
When a thin liquid film flows down on a vertical fiber, one can observe the complex and captivating interfacial dynamics of an unsteady flow. Such dynamics are applicable in various fluid experiments due to their high surface area-to-volume ratio. In this project, we study a mathematical model and present a computationally efficient numerical method that can maintain physical properties of the liquid films.
Barcode Image Analysis
Collaborating with
Dr. Yifei Lou (UT Dallas, Math)
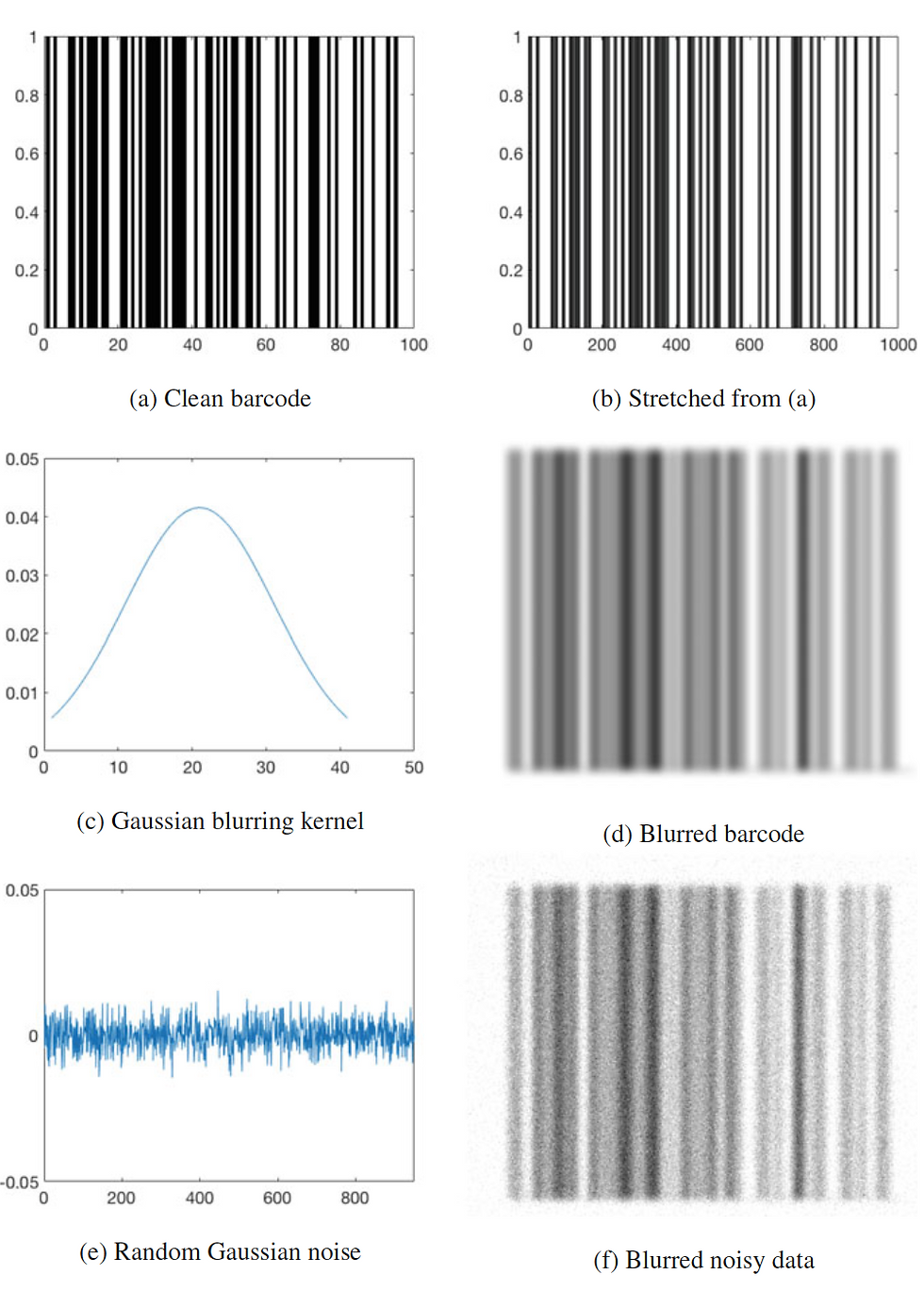
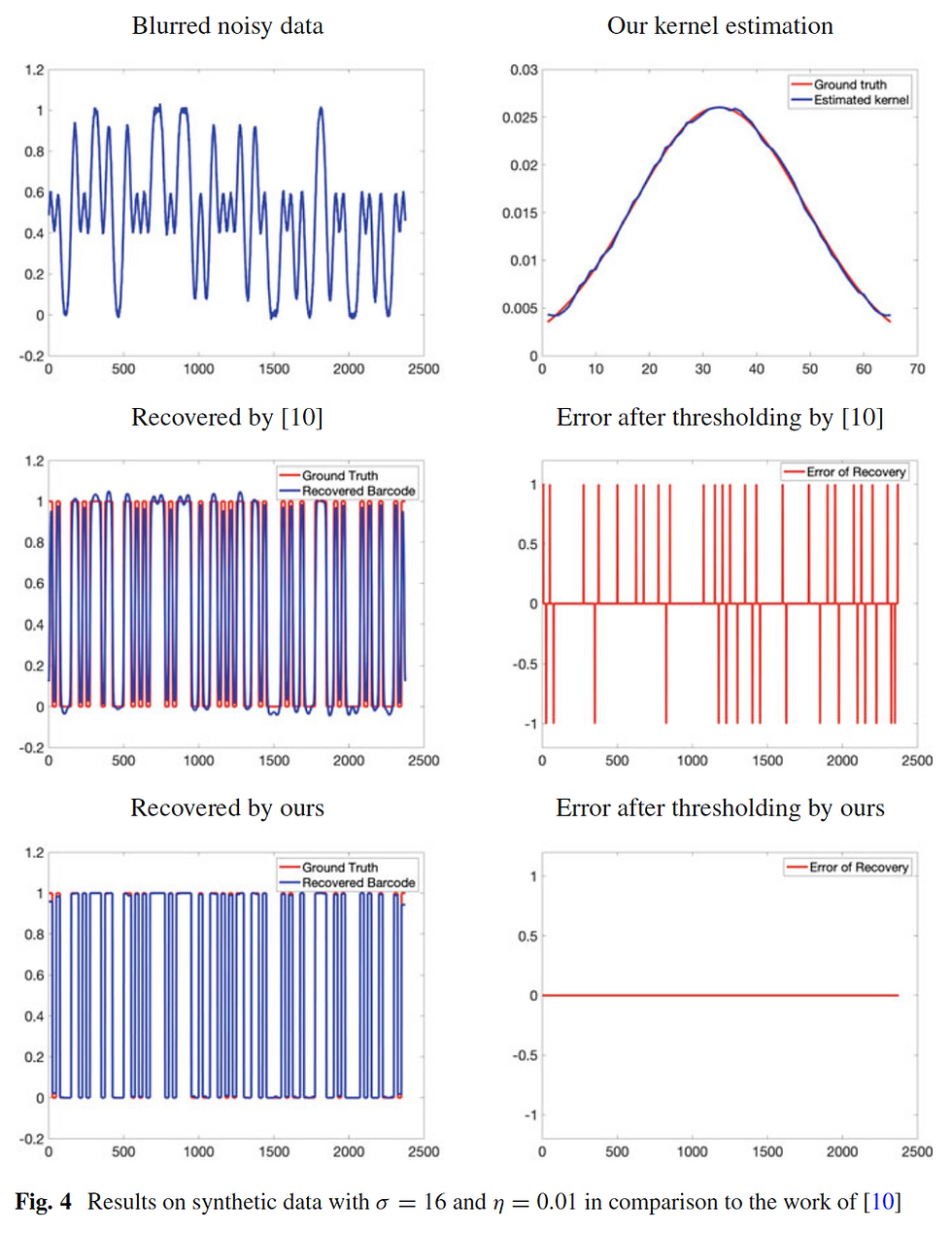
Kim, B., Lou, Y. (2021). Two-Step Blind Deconvolution of UPC-A Barcode Images. In: Demir, I., Lou, Y., Wang, X., Welker, K. (eds) Advances in Data Science. Association for Women in Mathematics Series, vol 26. Springer, Cham. [link][Software]
Barcodes are widely used in supermarkets and tracking systems. One noticeable difficulty in barcode recognition is caused by blurring artifacts. We propose a blind deconvolution method to recover a clean barcode from the blurred data.


Method of Particular Solutions (MPS)
Advising Seth Brown (University of Utah)
Our objective for Summer 2024 is to thoroughly understand and implement the Method of Particular Solutions (MPS), which has demonstrated strong numerical performance across various domains, including those with multiple singular corners and sharp edges. Currently, we are focusing on extending MPS to three-dimensional applications. [Software]


Me & Seth
Eigenfunctions for Laplace eigenvalue problem on L-shaped domain (Seth Brown)
Compressed Sensing (CS) method arising in Magnetic Resonance Imaging (MRI)
Advised by
Dr. Deanna Needell (UCLA, Math)
Collaborated with
Sam Birns, Stephanie Ku, Kevin Stangl.
Birns, S., Kim, B., Ku, S., and Stangl, K. (2016). A Practical Study of Longitudinal Reference-Based Compressed Sensing for MRI. Rose-Hulman Undergraduate Mathematics Journal: Vol. 17: Iss. 2, Article
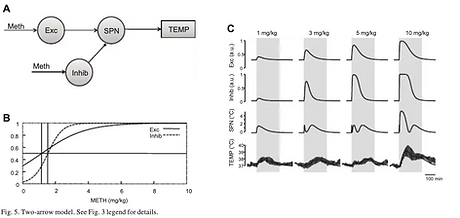
Mathematical modeling of thermoregulation
REU program hosted by Mathematical Bioscience Institutes (MBI)
Advised by
Dr. Yaroslav Molkov
Image from
Molkov, Y. I., Zaretskaia, M. V., & Zaretsky, D. V. (2014). Meth math: modeling temperature responses to methamphetamine. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology, 306(8), R552-R566.